Author: Zsófia Ruttkay Version: 1.0 Date: 25.2.2009
In nature you often see that parts of a structure are smaller - exact or slightly changed - copies of the entire structure. Think of branching trees, snow-flakes or clouds.
The basic principle is self-similarity which can be programmed elegantly by using recursion .
Self-similarity
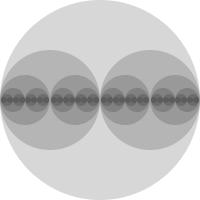
| Two circles inside one
The recursive production rule is to draw two half-sized circles in the 'parent'. | ellipse() |

|
Same rule as above, but the location of the smaller circles is changed. | |
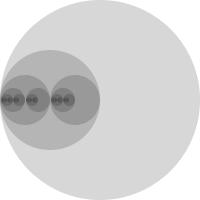
|
Watch out! Is this structure self-similar? Could you alter the code to produce a recursive one? | |
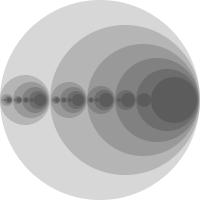
|
How about this one? | |

|
Explain why the previously seen logarithmic spiral is a recursive structure. | |
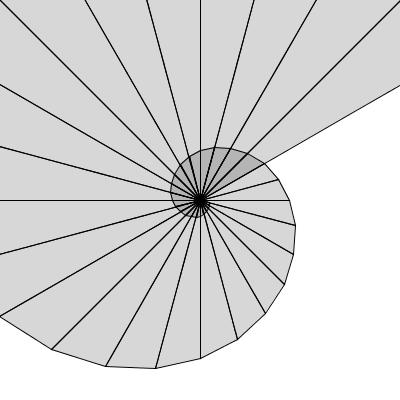
|
Same as the previous structure, but triangles are drawn. Looks like a shelf. |
Trees

| Tree by D. Shiffman
A fully symmetrical tree. | pushMatrix(), popMatrix(), translate(), rotate() |
| Asymmetric tree
.. with different angles for left and right branching. | |

| Asymmetric tree driven by mouse
Mouse Y defines basic branching, mouseX the amount of asymmetry. | |

| Tree with leaves
Square leaves added to Tree0. | |

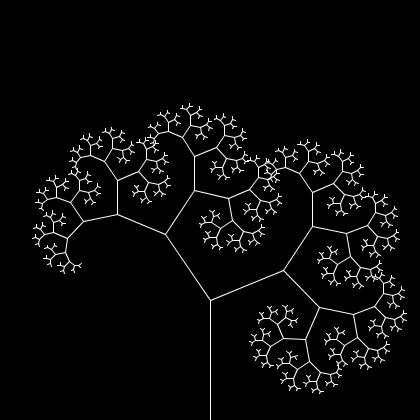
| Naked tree of Pythagoras
Left and right branching angles add up to PI/2. What is the scale? | |
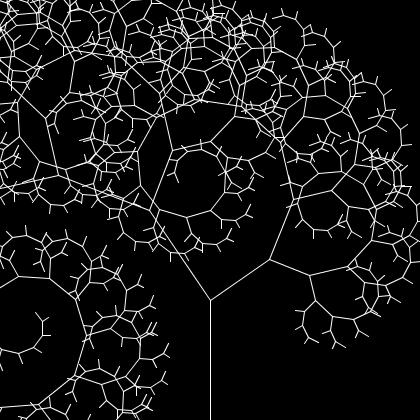
|
As above, but left and right branch scales differ. | |

| Tree with random variation
| |

| Make a forest
On mouse-click a new tree is planted. Size is proportional to y location. | |

| Symmetrical, generalized Pythagoras tree
Angle is decided by mouseX. | |

| Asymmetrical tree or Pythagoras
| |

| A different visualisation of the tree of Pythagoras
| |
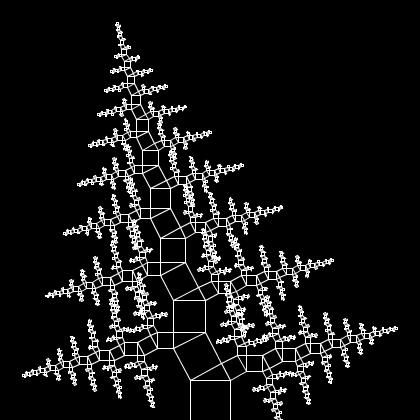
| Tree of Pythagoras with alternating left-right angles
Create variants with moving the mouse. Looks like a fern! |