Author: Zsófia Ruttkay Version: 1.0 Date: 25.2.2009

One of the problems with computer-generated forms and motions is that they are too regular and too perfect: no small deviations, no sketch-like lines, no individual subtle characteristics of motion. Moreover, at each time a generative code is run, the result is always the same: identical structures and textures, repetition of identical steps in motion. Unless we do something about it.

Yes, we can add a more natural character to computer-generated artifacts, by just breaking the neatness of the fully deterministic programs by exploiting noise. Noise ...? Non-determinism? The things you probably would expect the least beneficial in a computer program.

We already saw how beneficial it is to design and code forms in a parametrisable way, and then select a value randomly for some parameters, resulting in different forms and structures each time - see e.g. Flower??, Tree??. Now we will have control over noise. We will see how to create 'irregular' but reproducible - that is, for each run the same - results. Moreover, by using Perlin-noise, we will be able to influence the amount of irregularity.

Finally, you will see that the very same mathematical idea of the Perlin noise can be used to produce variety in a different media, to produce lines and forms, sound, 2d textures, and ... change these smoothly in time, resulting in natural-looking motion of clouds or a waterfall.

Randomness

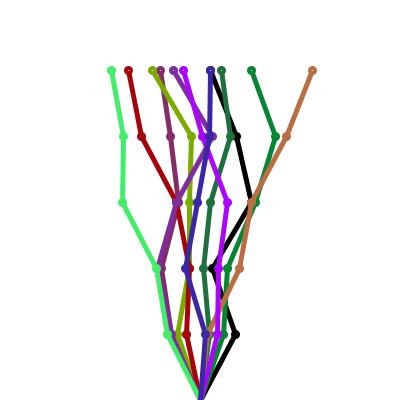
	Random stems by varying segment coordinates The x coordinate of the segment joints is chosen randomly. Much zig-zag may occur. src: CourseSketches/Noises/randomstem1/randomstem1.pde	random()
	Random stems with different segment numbers, and decreasing random deviation in x. Mod of previous. The number of segments is chosen randomly, size different. Joint deviation changes according to cos() function. src: CourseSketches/Noises/randomstem2/randomstem2.pde	random(...)*cos(...)
	Random stems with different number of segments of identical y-length Mod of previous. The y length of segments is identical for each branch. src: CourseSketches/Noises/randomstem3/randomstem3.pde	random()
	Random stems growing left or right Mod of previous. The branches go left or right, this is decided for each branch randomly too. src: CourseSketches/Noises/randomstem4/randomstem4.pde	random()
	Leaves Mod of previous. The branch segments are drawn with quad(), giving width, looking more like leaves. src: CourseSketches/Noises/randomstem5/randomstem5.pde	quad()
	Pointed leaves Mod of previous. Leaves are pointed at end by reducing width there to 0. Tints of green as color. src: CourseSketches/Noises/randomstem6/randomstem6.pde
	Grass Mod of previous. Now the x coordinate of the root for each branch is selected randomly, and the minimum number of segments is 3*/4 of the max nof segments, given by nofSegments. src: CourseSketches/Noises/randomstem7/randomstem7.pde
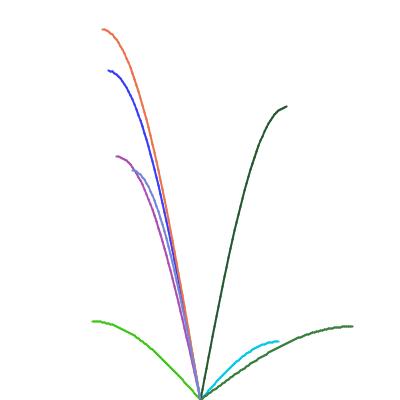
	Smoothly curved random stems The stems are all sinusoid shapes. The x and y directional scaling is chosen randomly. src: CourseSketches/Noises/sinusstem1/sinusstem1.pde	random(), a*sin(x/b) drawing sin() function
	Smoothly curved random leaves Mod of previous, and analog of randomsetm6. A leaf is enclosed by sin() and sin()*sin() curves. src: CourseSketches/Noises/sinusstem2/sinusstem2.pde	sin()*sin()
	Smoothly curved random leaves, filled Mod of previous, and analog of randomsetm7. A leaf is drawn by filled quad() pieces. src: CourseSketches/Noises/sinusstem3/sinusstem3.pde	quad()
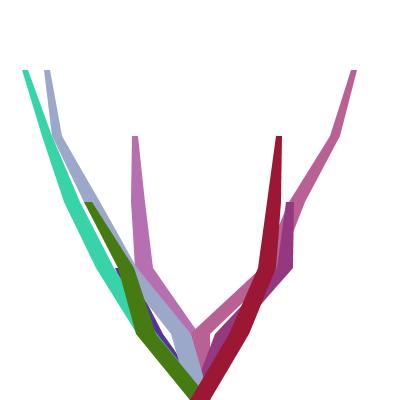
	Random, but reproducible results You can assure that the same set of random values are produced by random() calls by giving a 'seed' for the random generator at the beginning. Experiment with setting the seed variable to 122,152, or other values. src: CourseSketches/Noises/randomstem8/randomstem8.pde	randomSeed()

Using Perlin noise

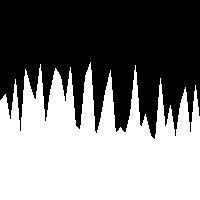
	Random peaks Random zig-zag mountain silhouette, by choosing peak heights between min and max values randomly. Step size (dx) is 5. src: CourseSketches/Noises/randompeaks1/randompeaks1.pde	random()
	Random peaks rough Mod of previous, producing rougher skyline. Only change is that step size (dx) is 5. src: CourseSketches/Noises/randompeaks2/randompeaks2.pde	random()
	Peaks with one dimensional Perlin noise The 1d panoramic view of peaks is produced by using the noise(t) function. More coherent look. src: Shiffman/noisegraph/noisegraph.pde	noise(t)
	Peaks with one dimensional Perlin noise and adjustable details Same as previous, except the noiseDetail(8,0.5) function defined the amplitude and effect of noise components. Experiment with changing the 2 parameters one by one. src: Shiffman/noisegraph2/noisegraph2.pde	noiseDetail(amp,effect), noiseSeed()
	2D Perlin noise Pixels grey level is defined by 2d Perlin noise. Noise character is defined by noiseDetail( amp, effect) as in previous sketch. By using noiseSeed(), the same noise is generated in each run. On mouse click noise detail changes. src: Shiffman/noise2D/noise2D.pde	noise(x,y), noiseDetail(amp,effect), noiseSeed()
	Texture modifications with 2D Perlin noise A striped texture created with sin() is deformed by 2D Perlin noise. Two parameters define density and power of the deformation introduced by noise(x,y). By mouse click these parameters are made from mouse location. You can explore the program by changing varaible values. src: CourseSketches/Noises/Mod15_10/Mod15_10.pde	noise(x,y)
	2d texture animation with 3D Perlin noise 3D Perlin noise generated at (x,y,t) coordinates defines the grey level at (x,y) in time t. Can you imagine using 4D Perlin noise to animate changing 3D surface? In processing only up to 3 dimensional Perlin noise is incorporated, though. src: CourseSketches/Noises/Mod32_09/Mod32_09.pde	noise(x,y,z)

On-line learning resources

Wikipedia random walk page

Introduction to Perlin-noise by D. Shiffman with Processing code examples (at the bottom of the page).

Paul Bourke's site first part explaining the principle and illustrating with figures and images

Making Noise by Ken Perlin

Further links